2023년 9급 국가직 공무원 무선공학개론 기출해설

 

무선공학개론 연도별 해설(07-23 국가직)https://kmong.com/gig/550928

무선공학개론 연도별 해설(15-23 해경직) https://kmong.com/gig/550934

무선공학개론 단원별 해설(07-23 국가직, 15-23 해경직) https://kmong.com/gig/572146

1번 문제

새넌의 채널 용량 공식을 따를 때, 동일한 시간에 가장 많은 데이터를 전송할 수 있는 무선통신 시스템은?

1) 대역폭: 500[MHz], 신호대잡음비: 63

2) 대역폭: 600[MHz], 신호대잡음비: 31

3) 대역폭: 400[MHz], 신호대잡음비: 127

4) 대역폭: 800[MHz], 신호대잡음비: 15

[해설] 답 : 4번

섀넌 채널용량 공식

\(C=B\times log_2(1+SNR)\)

C: 채널용량, B: 대역폭, SNR: 신호대잡음비

1. \(C=500\times log_2(1+63)\)
2. \(C=600\times log_2(1+31)\)
3. \(C=400\times log_2(1+127)\)
4. \(C=800\times log_2(1+15)\)

따라서 4번이 가장 큰 채널 용량을 갖습니다.

 

2번 문제

전파의 특성에 대한 설명으로 옳지 않은 것은?

1) 파장이란 주기적으로 변화하는 에너지 레벨이 한 주기 동안 지행한 거리이다.

2) 회절이란 경계면에 도달한 전파가 새로운 파원이 되어 진행하는 현상을 말한다.

3) 전파의 직진과 반사의 특성을 이용한 것으로는 레이더가 있다.

4) 전파의 주파수가 높을수록 회절이 잘되고 낮을수록 직진성이 좋아진다.

[해설] 답 : 4번

1. 파장: 파장은 주기적으로 변화하는 에너지 레벨이 한 주기 동안 진행한 거리로 정의됩니다. 이 설명은 정확합니다.
2. 회절: 회절은 경계면에 도달한 전파가 새로운 파원이 되어 진행하는 현상을 의미합니다. 이것은 전파의 중요한 특성 중 하나이며, 설명은 정확합니다.
3. 전파의 직진과 반사: 전파의 직진과 반사의 특성은 레이더 기술에서 중요한 역할을 합니다. 이 설명도 정확합니다.
4. 주파수와 회설/직진성: 전파의 주파수가 높을수록 회절이 잘되고, 낮을수록 직진성이 좋아진다는 설명은 잘못되었습니다. 실제로는 주파수가 낮을수록 회절이 잘되고, 높을수록 직진성이 강해집니다.

따라서 정답은 4번입니다.

 

3번 문제

OFDM을 사용하는 시스템에 대한 설명으로 옳지 않는 것은?

1) 다수 개의 부반송파를 사용하여 레이더를 전송한다.

2) 심벌 간 간섭을 완화하기 위해 보호구간을 삽입한다.

3) 단일반송파 전송 방식에 비해 최대전력 대 평균전력비가 낮다.

4) 고속 푸리에 역변환을 사용하여 OFDM 변조 기능을 구현할 수 있다.

[해설] 답 : 3번

1. 다수 개의 부반송파 사용: OFDM 시스템은 데이터 전송을 위해 다수의 부반송파를 사용합니다. 이 설명은 정확합니다.
2. 보호구간 삽입: OFDM 시스템에서는 심벌 간 간섭을 완화하기 위해 보호구간을 삽입합니다. 이것도 정확한 설명입니다.
3. 최대전력대 평균전력비: OFDM 시스템은 단일반송파 전송 방식에 비해 최대전력 대 평균전력비(Peak-to-Average Power Ratio, PAPR)가 높은 것으로 알려져 있습니다. 따라서 이 설명은 잘못되었습니다.

 

4번 문제

위성통신에 대한 설명으로 옳지 않은 것은?

1) 위성과 지구국의 양각이 증가할수록 왕복지연시간이 짧아진다.

2) 저궤도 위성통신은 정지궤도 위성통신보다 왕복지연시간이 짧다.

3) 위성통신에서 사용되는 C밴드는 4~8[GHz] 주파수 범위를 갖는다.

4) 일반적으로 상향링크보다 하향링크에서 더 높은 주파수를 사용한다.

[해설] 답 : 4번

일반적으로 상향링크(지구국에서 위성으로 보내는 신호)는 하향링크(위성에서 지구국으로 보내는 신호)보다 낮은 주파수를 사용합니다. 따라서 이 선지는 옳지 않습니다.

 

5번 문제

디지털 통신시스템의 수신 신호전력을 S [W], 잡음전력을 N [W], 전송 채널 대역폭을 W [MHz], 비트 전송률을 R [MHz]이라고 할 때, 비트에너지 대 잡음전력밀도 \(\frac{E_b}{N_o}\)가 가장 큰 것은?

1) S: 1, N: 2, W: 4, R: 1

2) S: 1, N: 2, W: 2, R: 4

3) S: 2, N: 1, W: 2, R: 1

4) S: 2, N: 1, W: 1, R: 2

[해설] 답 : 3번

비트에너지 대 잡음전력밀도(Eb/N0)는 수신 신호전력(S), 잡음전력(N), 전송 채널 대역폭(W), 그리고 비트 전송률(R)에 따라 결정됩니다.

\(\frac{E_b}{N_o}=\frac{S/R}{N/W}=\frac{S}{R\times N/W}\)

1. 2
2. 1/4
3. 4
4. 1

 

6번 문제

송신기는 300[MHz]의 주파수와 16[W]의 전력을 사용하여 자유 공간으로 신호를 전송한다. 송신안테나와 수신안테나의 이득이 각각 30[dB]일 때, 송신기로부터 1[km] 떨어진 지점에 수신되는 전력[W]은? (단, 전파속도는 \(3\times 10^8\)[m/s]이고, 주어진 조건 외의 영향은 고려하지 않는다)

1) \(\frac{1}{\pi^2}\)

2) \(\frac{8}{\pi^2}\)

3) \(\frac{16}{\pi^2}\)

4) \(\frac{30}{\pi^2}\)

[해설] 답 : 1번

안테나 이득을 선형 값으로 변환: dB 값은 로그 스케일을 나타내므로, 이를 선형 스케일로 변환해야 합니다. 이를 위해 10의 (dB 값 / 10) 제곱을 취합니다.

\(30[dB]->10^3=1,000\)

수신 전력 계산: 프리스 전송 방정식에 따라, 수신 전력은 송신 전력, 안테나 이득, 신호의 파장(빛의 속도를 주파수로 나눈 값), 그리고 거리를 고려하여 계산됩니다.

\(Pr=Pt\times Gt\times Gr\times (\frac{\lambda }{4\pi d})^2\)

Pr: 수신전력, Pt: 송신전력, Gt, Gr: 송수신 안테나 이득

\(\lambda \): 파장, d: 거리

\(\lambda =\frac{c}{f}=1\)

\(Pr=16\times 10^3\times 10^3\times (\frac{1}{4\pi \times 1000})^2\)

 

7번 문제

주파수가 20[kHz]인 정현파 신호를 100[MHz]의 반송파로 주파수 변조하여 최대 주파수 편이가 500[kHz]가 되었다. 카슨(Carson) 법칙을 이용하여 구한 변조 신호의 대역폭과 변조지수를 바르게 연결한 것은?

1) 대역폭: 1040[kHz], 변조지수: 25

2) 대역폭: 1040[kHz], 변조지수: 200

3) 대역폭: 520[kHz], 변조지수: 25

4) 대역폭: 520[kHZ], 변조지수: 200

[해설] 답 : 1번

대역폭 계산: 카슨의 법칙에 따라 변조 신호의 대역폭은 2배의 (최대 주파수 편이 + 원래 신호의 최대 주파수)입니다.

대역폭\(=2\times (500+20)=1040kHz\)

변조지수 계산: 변조지수는 주파수 편이를 원래 신호의 최대 주파수로 나눈 값입니다.

변조지수=\(\frac{500}{20}=25\)

 

8번 문제

디지털 변조 방식인 ASK, PSK, FSK 및 QAM에 대한 설명으로 옳지 않은 것은?

1) 이진 변조와 동기식 복조를 사용할 때, 동일한 비트오율을 얻기 위한 \(E_b/N_0\)는 PSK 방식이 FSK 방식에 비해 작다.

2) ASK와 FSK는 비동기 복조가 가능하므로 수신기의 복잡도를 낮출 수 있다.

3) 임의의 \(E_b/N_0\) 에서 QPSK는 BPSK와 동일한 비트오율 성능을 얻을 수 있지만 대역폭 효율은 감소한다.

4) M진 QAM에서 M을 증가시킬 경우, 심벌당 전송할 수 있는 비트 수가 증가하여 대역폭 효율이 개선된다.

[해설] 답 : 3번

PSK와 FSK의 비트오율: 이진 변조와 동기식 복조를 사용할 때, PSK 방식이 FSK 방식에 비해 더 작은 비트 에너지 대 잡음전력비(Eb/N0)로 동일한 비트오율을 얻을 수 있다는 설명은 올바릅니다.

ASK와 FSK의 복잡도: ASK와 FSK가 비동기 복조가 가능하다는 설명은 옳습니다. 이로 인해 수신기의 복잡도를 낮출 수 있습니다.

QPSK와 BPSK의 비트오율과 대역폭 효율: 임의의 Eb/N0에서 QPSK는 BPSK와 동일한 비트오율 성능을 얻지만 대역폭 효율은 감소하지 않습니다. QPSK는 BPSK에 비해 대역폭 효율이 두 배 높습니다.

M진 QAM의 대역폭 효율: M진 QAM에서 M을 증가시킬 경우 심벌당 전송할 수 있는 비트 수가 증가하여 대역폭 효율이 개선된다는 설명은 올바릅니다.

3번 선택지가 옳지 않은 설명입니다. QPSK는 BPSK와 동일한 비트오율 성능을 갖지만, 대역폭 효율이 감소한다는 부분이 잘못되었습니다. 실제로 QPSK는 BPSK에 비해 대역폭 효율이 더 높습니다.

 

9번 문제

송신기의 출력단은 특성임피던스 50[Ω]인 무손실 동축케이블과 완벽하게 정합되어 있고, 동축케이블은 입력임피던스가 30[Ω]인 안테나와 연결되어 있다. 송신기에서 안테나로 64 [W]의 신호전력을 전송할 때, 송신기로 반사되는 신호전력[W]은?

1) 2

2) 4

3) 8

4) 10

[해설] 답 : 2번

반사계수(Γ) 계산: 반사계수는 부하 임피던스(안테나 임피던스)와 소스 임피던스(특성 임피던스)의 차이를 바탕으로 계산됩니다.

Γ=\(|\frac{Z_l-Z_o}{Z_l+Z_o}|=\frac{1}{4}\)

\(Z_l\) : 안테나 임피던스, \(Z_0\): 특성 임피던스

반사된 신호전력 계산: 반사된 전력은 반사계수의 제곱에 전송된 전력을 곱한 값입니다

반사된 전력= Γ^2 전송된 전력=\((\frac{1}{4})^2\times 64=4[W]\)

 

10번 문제

그림과 같이 주기 T가 200[\(\mu s\)]인 사각파 정보신호를 1[MHz]의 반송파로 진폭 변조할 때, 변조된 신호에 나타나지 않는 주파수[kHz]는?

1) 995

2) 1005

3) 1010

4) 1015

[해설] 답 : 3번

사각파 신호의 기본 주파수 계산: 사각파의 기본 주파수는 신호의 주기의 역수입니다.

\(f=\frac{1}{200\mu }=5[kHz]\)

홀수 배수 주파수 계산:진폭 변조된 사각파 신호는 기본 주파수와 그 홀수 배수를 포함합니다. 

따라서 1010[kHz]인 10의 배수는 해당되지 않습니다.

 

11번 문제

비유전율 \(\epsilon _r\) 이 64이고 비투자율 \(\mu_r\)이 4인 매질에서 진행하는 전파 이동속도는 자유공간에서 진행하는 전파 이동속도의 몇 배인가?

1) 16

2) 4

3) 1/4

4) 1/16

[해설] 답 : 4번

매질에서의 전파 속도 계산: 매질에서의 전파 속도는 자유공간에서의 전파 속도를 비유전율(εr)과 비투자율(μr)의 제곱근으로 나누어 계산합니다.

\(v=\frac{c}{\sqrt{\epsilon _r\mu _r}}=\frac{3\times 10^8}{\sqrt{64\times 4}}=\frac{3}{16}\times 10^8[m/s]\)

자유공간 대비 매질에서의 전파 속도 비율 계산: 이 비율은 매질에서의 전파 속도를 자유공간에서의 전파 속도로 나누어 계산합니다.

따라서 매질에서의 전파 이동속도는 자유공간에서의 전파 이동속도의 1/16(0.0625) 배입니다.

 

12번 문제

마이크로파 신호의 무선 전파 환경에 대한 설명으로 옳지 않은 것은?

1) 통신거리가 증가함에 따라 전파의 세기가 감소하는 현상을 경로 손실이라고 한다.

2) 백색가우시안 잡음의 주요 원인은 다른 사용자들로부터 송신되는 전파에 의한 방해이다.

3) 건물, 지형 등 장애물에 의해 수신신호의 평균전력이 달라지는 현상을 섀도윙이라고 한다.

4) 송신 신호의 회절, 반사, 산란 등에 의해 다중 경로가 발생한다.

[해설] 답 : 2번

경로 손실: 통신 거리가 증가함에 따라 전파의 세기가 감소하는 현상을 ‘경로 손실’이라고 합니다. 이 설명은 정확합니다.

백색가우시안 잡음: 백색가우시안 잡음의 주요 원인이 다른 사용자들로부터 송신되는 전파에 의한 방해라는 설명은 잘못되었습니다. 백색가우시안 잡음은 주로 자연적인 전자기적 환경에서 발생하는 무작위적인 잡음입니다.

섀도윙: 건물, 지형 등 장애물에 의해 수신 신호의 평균 전력이 달라지는 현상을 ‘섀도윙’이라고 합니다. 이 설명은 정확합니다.

다중 경로: 송신 신호의 회절, 반사, 산란 등에 의해 다중 경로가 발생한다는 설명은 정확합니다.

 

13번 문제

주로 밀리미터파 응용 및 레이더에 사용되는 무선 주파수 대역은?

1) EHF

2) VLF

3) HF

4) UHF

[해설] 답 : 1번

EHF (Extremely High Frequency): 이 대역은 30~300 GHz에 해당하며, 밀리미터파에 해당합니다. 밀리미터파와 레이더에 널리 사용됩니다.

VLF (Very Low Frequency): 3~30 kHz의 매우 낮은 주파수 대역입니다.

HF (High Frequency): 3~30 MHz의 고주파수 대역입니다

UHF (Ultra High Frequency): 300 MHz~3 GHz의 초고주파수 대역입니다.

 

14번 문제

지구국과 12[GHz]의 주파수로 통신하는 정지궤도위성이 최대 10[kHz]의 주파수 편이를 허용할 때, 위성과 통신 연결을 유지할 수 있는 지구국의 최대 이동속도[m/s]는? (단, 전파속도는 \(3\times 10^8[m/s]\)이다.)

1) 100

2) 150

3) 200

4) 250

[해설] 답 : 4번

ㅇ도플러 효과: 이 문제는 도플러 효과를 이용하여 풀 수 있습니다. 도플러 효과는 관찰자와 소스 사이의 상대적 움직임에 따라 관측되는 주파수가 변화하는 현상입니다.

ㅇ주파수 편이: 주파수 편이\(\Delta f\) 관측된 주파수와 실제 주파수의 차이입니다.

ㅇ이동속도 계산: 최대 주파수 편이 \(\Delta f\)를 이용하여 지구국의 최대 이동속도를 계산할 수 있습니다.

\(v=\frac{\Delta f\times c}{f}=\frac{10k\times 3\times 10^8}{12G}\simeq 250m/s\)

 

15번 문제

펄스폭이 1\([\mu s]\)이고 펄스 반복 주파수가 300[Hz]인 펄스 레이더의 거리 분해능[m]은? (단, 전파속도는 \(3 \times 10^8\)[m/s]이다)

1) 100

2) 150

3) 200

4) 250

[해설] 답 : 2번

ㅇ펄스 레이더의 거리 분해능 계산: 거리 분해능은 전파 속도와 펄스폭을 고려하여 계산됩니다. 공식은 다음과 같습니다

거리분해능=c x 펄스폭/2\(=\frac{3\times 10^8\times 1\mu }{2}=150\)

 

16번 문제

그림은 이동통신 시스템에서 주파수 재사용을 위해 인접한 3개의 셀을 하나의 클러스터로 구성한 것이다. 셀 반경이 2[km]이고 각 셀에 주파수 대역폭을 균등하게 할당할 때, 동일 주파수 대역을 사용하는 셀 중심 간 최소거리[km]는? (단, 셀은 그림에 도식된 6각형 1개를 의미한다)

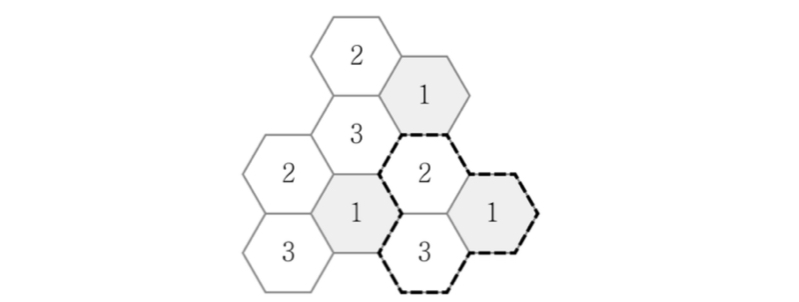
1) 6

2) 7

3) 8

4) 9

[해설] 답 : 1번

ㅇ셀 반경이 2km일 때, 인접한 3개의 셀을 하나의 클러스터로 구성합니다.

ㅇ이 경우, 동일 주파수 대역을 사용하는 셀 중심 간 최소 거리는 셀의 반경의 3배입니다. 이는 정육각형 셀의 기하학적 배치로부터 유도됩니다.

ㅇ따라서 동일 주파수 대역을 사용하는 셀 중심 간 최소 거리는\(2km\times 3=6km\)

 

17번 문제

정보신호 \(m(t)=2+5sin(2\pi t)\)를 반송파 전송 양측파대(DSB -TC, double sideband-transmitted carrier) 방식으로 변조하여 \([A_c+m(t)]cos(2\pi f_ct)\)신호를 생성할 때, 포락선 검파가 가능하도록 하는 \(A_c\)의 최솟값은?

1) 1

2) 2

3) 3

4) 4

[해설] 답 : 3번

포락선 검파가 가능하도록 하기 위해서는 반송파의 진폭 \(A_c\)가 정보신호의 진폭 \(A_m\)보다 크거나 같아야 합니다.

따라서 \(A_c+A_m\geq 0\)이므로 \(A_m\)이 최솟값 -3 일 때, \(A_c\)는 최솟값 3이 되야합니다.

 

18번 문제

반송파 억압 양측파대(DSB-SC, double sideband-suppressed carrier) 방식으로 변조된 신호 \(S_m(t)\)에 대한 복조기 구조가 그림과 같을 때, 곱셈기 출력 신호 y(t)의 스펙트럼 \(Y(f)\)는? (단, \(s_m(t)=m(t)cos(2\pi f_ct)\)이고, 정보신호 \(m(t)의 푸리에 변환은 M(f)이다)

1) \(M(f)+\frac{1}{2}M(f-f_c)+\frac{1}{2}M(f+f_c)\)

2) \(M(f)+\frac{1}{2}M(f-2f_c)+\frac{1}{2}M(f+2f_c)\)

3) \(\frac{1}{2}M(f)+\frac{1}{4}M(f-f_c)+\frac{1}{4}M(f+f_c)\)

4) \(\frac{1}{2}M(f)+\frac{1}{4}M(f-2f_c)+\frac{1}{4}M(f+2f_c)\)

[해설] 답 : 4번

복조된 신호는 다음과 같이 표현됩니다:

\(y(t)=s(t)\cdot cos(2\pi f_ct)=m(t)cos^2(2\pi f_ct)\)

따라서,\(y(t)=\frac{m(t)}{2}+\frac{m(t)\cdot cos(4\pi f_ct)}{2}\)

이 신호의 스펙트럼을 구하기 위해 푸리에 변환을 적용합니다. 첫 번째 항은 ( m(t) )의 스펙트럼 ( M(f) )을 주고, 두 번째 항은 ( M(f) )의 주파수가 ( \(2f_c\))만큼 이동한 버전을 제공합니다. 따라서, ( y(t) )의 스펙트럼 ( Y(f) )는 (\(M(f)\))와 ( \([M(f-f_c)+M(f+f_c)]/2\) )의 결합으로 표현됩니다.

 

19번 문제

등방성 방사기가 40[W]의 송신전력으로 신호를 방사할 때, 1[km] 떨어진 지점에서의 전력밀도[\(\mu\)W/m2]는?

1) \( \frac{2}{\pi } \)

2) \( \frac{5}{\pi } \)

3) \( \frac{10}{\pi } \)

4) \( \frac{20}{\pi } \)

[해설] 답 : 3번

구의 표면적 ( A )는 (\(4\pi r^2\) )로 계산됩니다. 여기서 ( r )은 구의 반지름, 즉 1km입니다. 따라서, \(A=4\pi(1000)^2\)

전력밀도 ( \(P_d\))는 전력 ( P )를 구의 표면적 로 나눈 값입니다.

즉,\(P_d=\frac{P}{A}=\frac{40}{4\pi \cdot 1000^2}=\frac{10}{\pi }[\mu W/m^2 ]\)

 

20번 문제

그림은 펄스부호변조(PCM, pulse code modulation)된 이진 데이터에 대해 차동 부호화(differential encoding)를 수행하는 과정이다. 이에 대한 설명으로 옳지 않은 것은?

1) 차동 부호화된 데이터에 양극성 NRZ를 이용하여 라인 코딩하였다.

2) 차동 부호화된 데이터에서 현재 비트의 전송 오류는 다음 비트의 검출에 영향을 주지 않는다.

3) 기준 비트를 제외한 차동 부호화된 데이터는 XNOR 연산으로 생성할 수 있다.

4) 수신기에서도 차동 방식으로 복호화를 수행한다.

[해설] 답 : 2번

선지 2번, “차동 부호화된 데이터에서 현재 비트의 전송 오류는 다음 비트의 검출에 영향을 주지 않는다”는 사실 옳지 않습니다. 차동 부호화 방식에서는 현재 비트의 오류가 이후의 비트에 영향을 미칠 수 있습니다. 이는 차동 부호화의 특성상, 각 비트가 이전 비트와의 차이로 표현되기 때문입니다. 따라서 하나의 비트에 오류가 발생하면, 이후 비트의 해석에도 영향을 미칠 수 있습니다.